The brain contains billions of neurons, so in theory we’d need a billion numbers to describe the brain’s activity. But in practice, we don’t need a billion numbers – just a handful often goes a long way. These numbers are said to define a low-dimensional manifold1 in neural space, and their existence implies that the brain typically visits only a small fraction of all its potential states. There is an analogous observation in evolutionary biology: The number of existing organisms is only a tiny fraction of all theoretically possible organisms. For example, there are no (and have never been) unicorns or centaurs, even though they are obviously conceivable to the human mind. In this blog pots, we will examine these analogous neural and evolutionary phenomena, and see what lessons can be draw from their similarity.

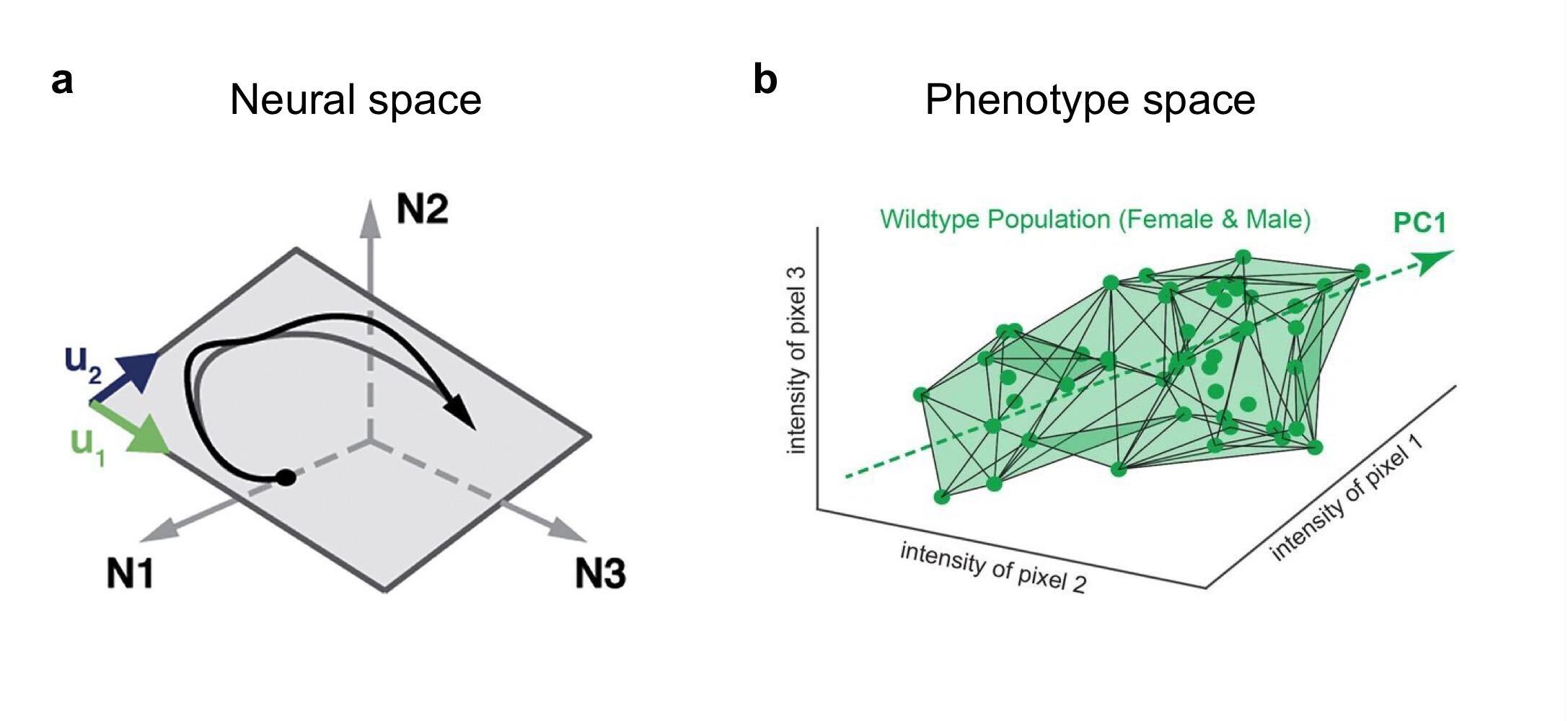(a) Population activity lies on a low-dimensional manifold in neural space. Each dimension corresponds to the activity of one neuron. (b) Variation of wing structure across a population of Drosophila lies on a low-dimensional manifold in phenotype space. Each dimension corresponds to the intensity of one pixel from an image of the wing. (a) From Gallego et al. 2017, (b) from Alba et al. 2021.

The full blog takes around 20 minutes to read. You can find a visual summary in this Twitter thread.

  1. Manifolds everywhere
  2. Explanation 1: function
  3. Explanation 2: constraint
  4. Probing neural manifolds
  5. Probing evolutionary manifolds
  6. Benefits of low-dimensionality
  7. Counterpoint: the case for high-dimensionality
  8. Takeaways for neuroscience
  9. Acknowledgements

Manifolds everywhere

The activity of a large number of neurons can often be captured by a much smaller number of key dimensions. In auditory cortex, for example, neural population activity rotates in a low-dimensional space determined by a stimulus-dependent initial condition (Bondanelli et al. 2021). In frontal cortex, the population’s initial state can depend on a subject’s prior expectations, allowing the dynamics to combine these expectations with sensory evidence (Sohn et al. 2019). Although in these and other cases, neural activity is not fully explained by two or three dimensions, these dimensions do explain a lot of variance, and relate to behavior in an interpretable way2. But human interpretability is not one of the brain’s design principles, raising the question why neural activity should be low-dimensional.

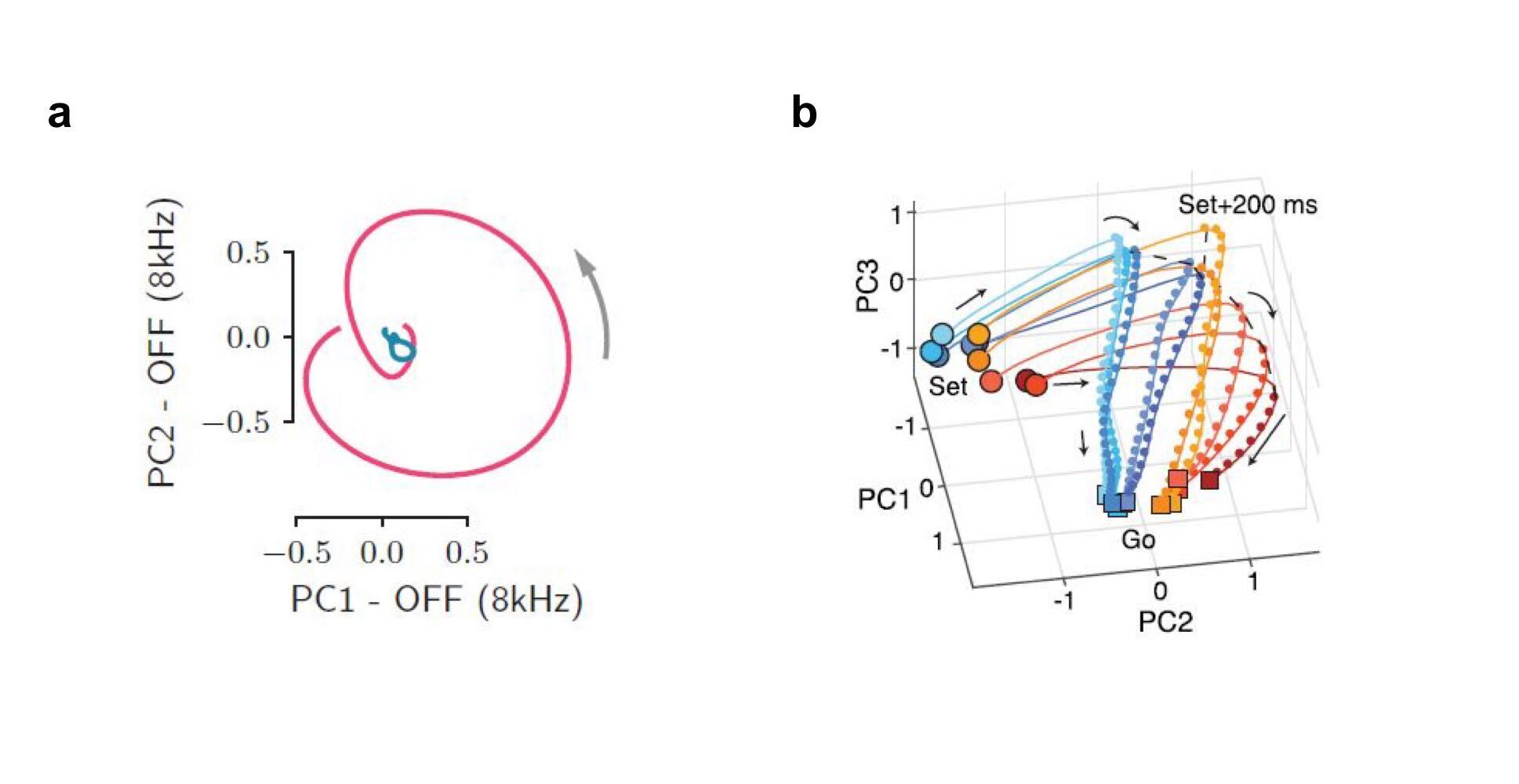(a) Two-dimensional rotations in auditory cortex after a sound is turned off. The two colours correspond to different sounds that elicited activity in orthogonal planes. (b) Activity in frontal cortex during the estimation of the time interval between a ‘Set’ and a ‘Go’ cue. The activity’s curvature depends on subjects’ prior expectations of the time interval (short prior: red, long prior: blue), and the actual duration of the interval (short duration: dark, long duration: light). (a) From Bondanelli et al. 2021, (b) from Sohn et al. 2019.

It’s much easier to observe and compare a lot of animals than to record from a lot of neurons, and that’s probably why comparative biologists have long known that phenotypes are also low-dimensional. For example, most mammals have seven neck vertebrae, even though the long-necked giraffe might benefit from more, and the neckless whale could do with less. In phenotype space, therefore, only the subspace of mammals with seven neck vertebrae is densely occupied. Within-species phenotypes can also be surprisingly low-dimensional: Fruit fly wings are well-approximated by a single dimension (Alba et al. 2021)! What causes such a sparse occupation of neural and phenotype spaces?

Explanation 1: function

The first explanation for low-dimensional patterns in neural and phenotype space is functional. Low-dimensional neural activity can result from low-dimensional neural computation: If a brain area is engaged in a simple computation (say, integrating a noisy variable over time), it’s activity will also be simple. This intuition was formalised by Gao et al., who showed that the number of task variables and the smoothness of neural activity necessarily limit the dimensionality of neural activity. The authors therefore concluded that (1) recording only a relatively small number of neurons compared to the full population is no problem, as long as the behavior is simple enough, but (2) more complex behaviours are necessary to fully exploit large-scale recordings. Since then, these ideas have become commonplace in systems neuroscience while the field has also realised that behavior can involve much more than the experimental task at hand (Musall et al. 2019, Stringer et al. 2019).

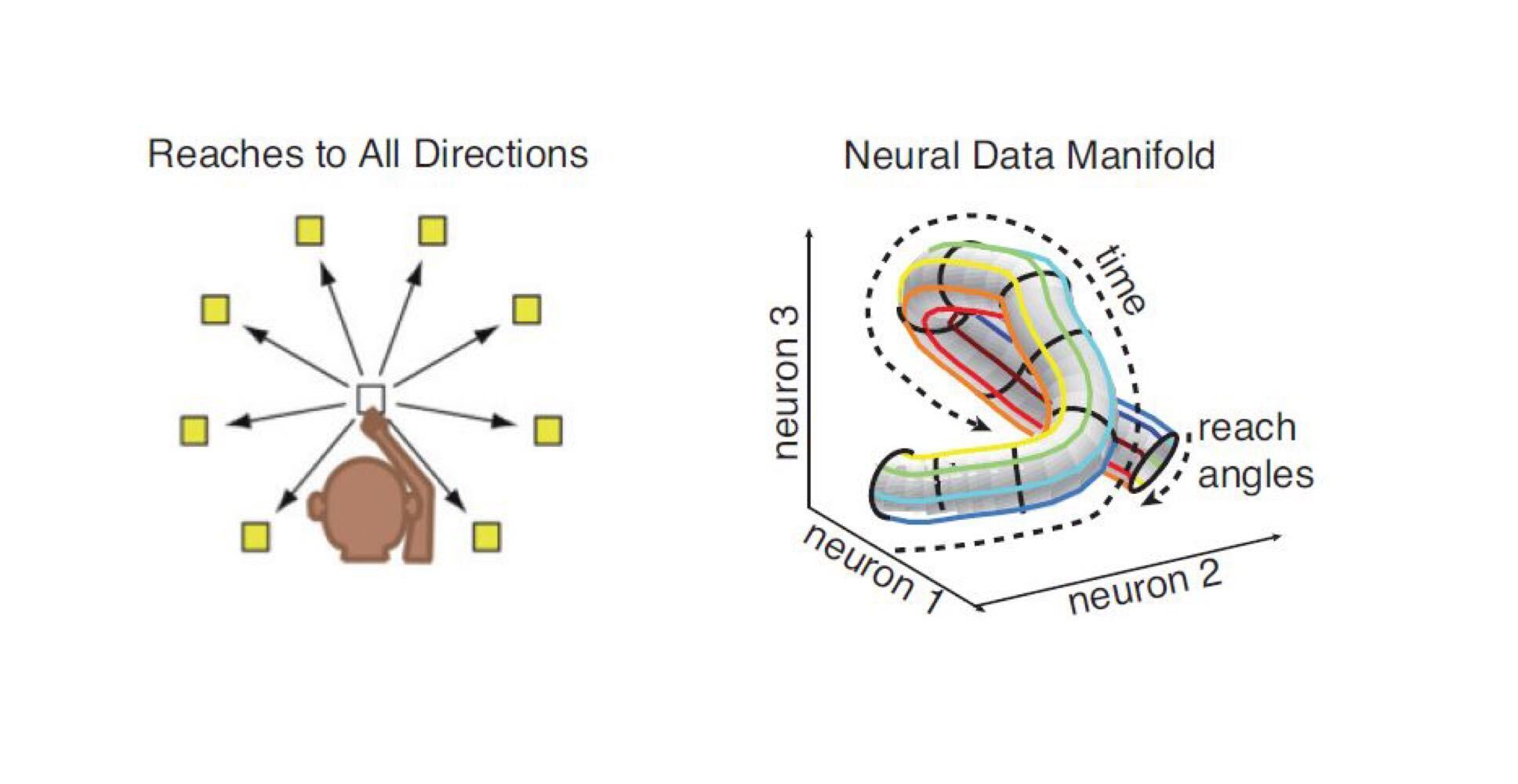If a subject is doing a relatively simple task like reaching, its neural activity varies smoothly in time, and we don’t record for very long – activity will be low-dimensional. From Gao et al. 2017.

Just like the brain learns to generate activity that’s suitable for the current task, natural selection favours variants that are fit to the current environment. If, therefore, only a few variants are the fittest, these are likely to spread through the population. In a famous example, black-coloured peppered moths used to be rare because they were easily spotted by predators when sitting on a light tree (Cook 2003). During the industrial revolution, however, pollution caused trees to be darker, making light-coloured moths the easier ones to spot. Natural selection therefore favoured black moths over their lighter brethren, making them the dominant variant. This pattern reversed once pollution decreased, providing one of the best-known examples of evolution in real time. At any given moment, selection might thus favour a limited set of phenotypes, making alternatives rare or non-existent. A similar pattern is seen at the level of genotypes: The genomes of all organisms lie on a low-dimensional manifold in ``sequence space’’. This is at least partly due to selection, since most mutations (i.e. deviations from the existing manifold) are known to decrease fitness. In sum, both neural activity and phenotypes are therefore limited to a small set of “optimal” patterns.

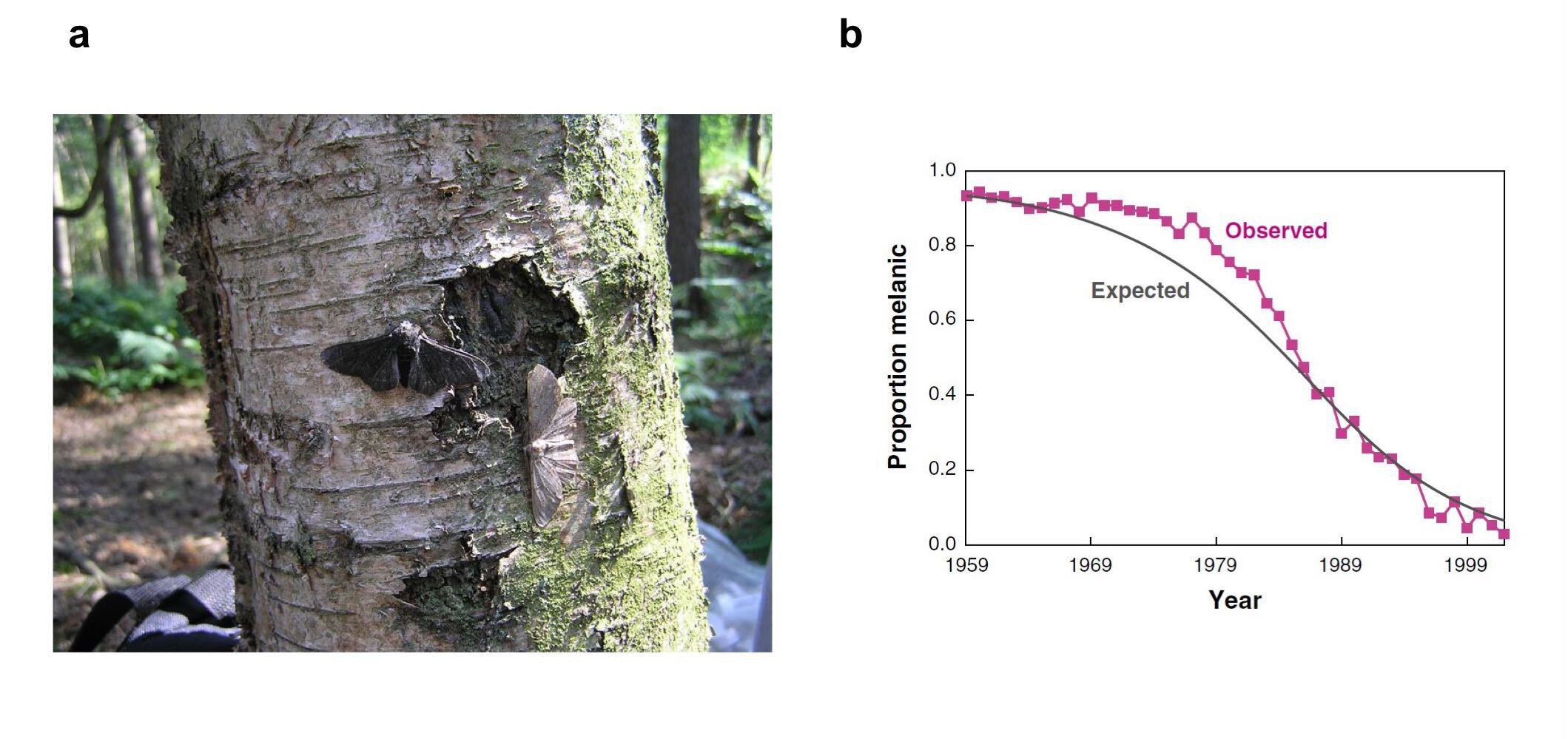(a) Peppered moths can have a light or a dark (melanic) colour. During the industrial evolution, air pollution made trees darker, and therefore decreased the visibility of melanic moths - increasing their fitness. (b) The pattern reversed when air pollution decreased. (a) from Wikipedia, (b) from Hedrick 2006.

Explanation 2: constraint

But sometimes the brain cannot produce a certain pattern of neural activity, even when it would be best to do so. Similarly, a certain phenotype might fail to evolve, even when it would increase a species’ fitness or even save it from extinction. In this case, the lack of variability must be due to the presence of constraints. For neural activity, such a constraint can be the synaptic connectivity. If, for example, two excitatory neurons are reciprocally connected, this might preclude activity patterns in which only one of them is active. Synaptic plasticity could weaken their connections, but this takes time. In the case of evolution, a constraint might be due to a single gene that affects multiple traits (pleiotropy), such that changing one trait but not the other is genetically impossible. A genetic constraint can also arise when two traits are coded for by different genes, but these genes are often inherited together, for example because they’re located nearby on the same chromosome. Over time, these constraints could be alleviated by mutations, but like synaptic plasticity, this takes time (a lot of time).

In sum, there are analogous reasons for low-dimensional patterns in neural space and animal space. This points to fundamental similarities between their origins. Neural activity is shaped by learning, and animal forms are shaped by natural selection. Both learning and natural selection tend to increase some kind of performance or fitness measure. But both are constrained in what they can achieve, especially in the short run.

Probing neural manifolds

Given that there are multiple possible causes of low-dimensional patterns, we would like to know which one is at play in any particular case. Neuroscientists and evolutionary biologists have conducted elegant experiments to test exactly this. In neuroscience, Sadtler et al. used a brain computer interface (BCI) to determine the neural constraints on learning. They started out by identifying a low-dimensional “intuitive manifold” of activity patterns that subjects could easily generate. This manifold was simply a principal subspace of subjects’ neural activity while they passively watched a cursor moving on a screen3. Next, the subjects had to actually control the cursor via a BCI mapping, by appropriately modulating their neural activity. After they’d learned this, the authors challenged their subjects to generate new activity patterns by changing (or ‘‘perturbing’’) the BCI mapping. Crucially, these changes came in two types: one type was inside the intuitive manifold, the other wasn’t. The inside manifold perturbation still projected neural activity onto the intuitive manifold, but then permuted the manifold dimensions before feeding them to the BCI mapping. Steering the cursor in a particular direction therefore required subjects to generate different activity than under the original mapping, but this activity could still be part of the intuivive manifold. The outside manifold perturbation, on the other hand, projected activity onto a subspace different from the intuitive manifold. In this case, controlling the cursor therefore required subjects to generate patterns that were not part of their original ``repertoire’’. The key finding from the experiment: Subjects could quickly adapt to inside manifold perturbations, but not to outside manifold perturbations. Thus, even when subjects should have broken free from the manifold, they didn’t. This suggests that the low-dimensionality of the intuitive manifold was not due to functional requirements, but rather to constraints.

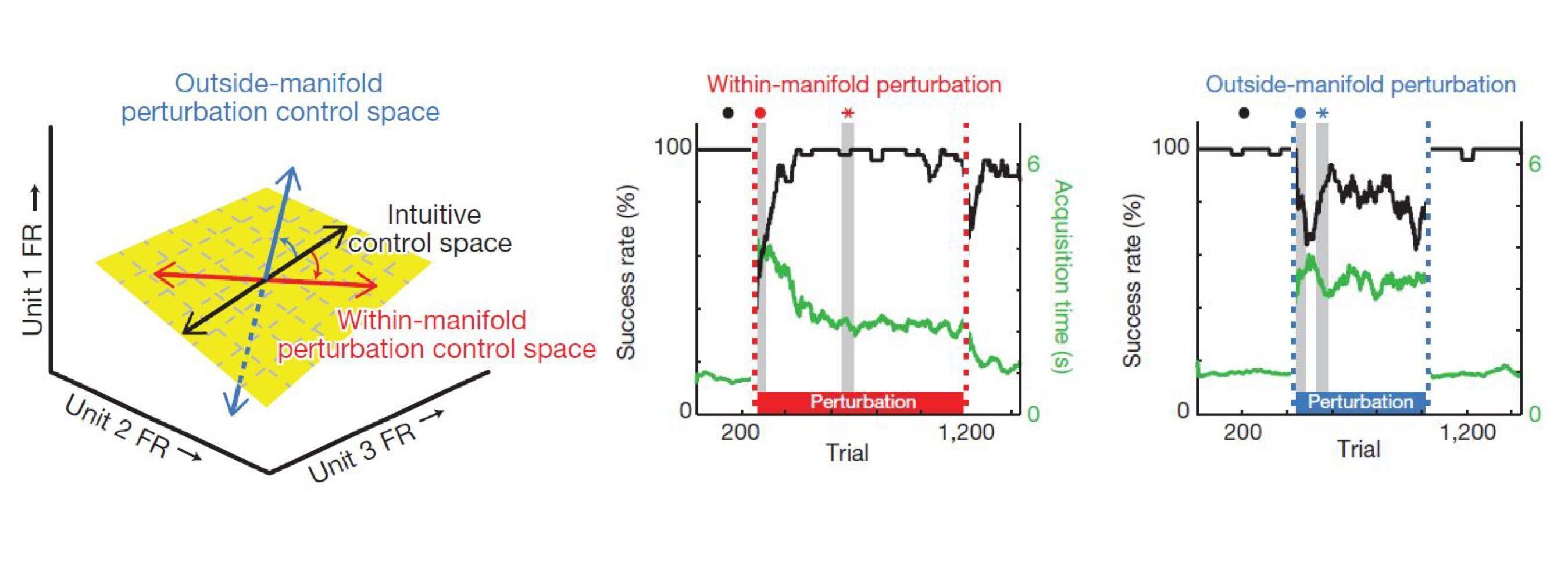Neural constraints on learning Sadtler et al. 2014. Neural activity is usually confined to an intuitive manifold. Changes to the BCI readout within this manifold (red) are easy to learn, changes outside the manifold (blue) are hard to learn.

Probing evolutionary manifolds

Evolutionary-developmental biologists have similarly tested the causes of low-dimensional phenotypes. Brakefeld et al. (Beldade et al. 2002, Allen et al. 2008) asked why the eyespots on the wings of a butterfly typically are similar in colour and size. Do similar eyespots convey a fitness advantage (e.g., asymmetric butterflies are picked out by predators), or do they naturally arise during development? Brakefeld et al. put this to the test in two artificial selection experiments. In one experiment, they selected butterfly strains for one of the four possible combinations of spot size: the two correlated combinations (small/small and large/large) and the two anti-correlated combinations (small/large and large/small). In another experiment, they selected butterflies based on eyespot colour. Interestingly, the two experiments showed opposite outcomes: It was possible to evolve anti-correlated spot sizes, but not colours. This suggests that similarly sized spots are the result of selection (different sizes are possible, but apparently not selected for), but similarly coloured spots are the result of constraints (different colours are not possible).

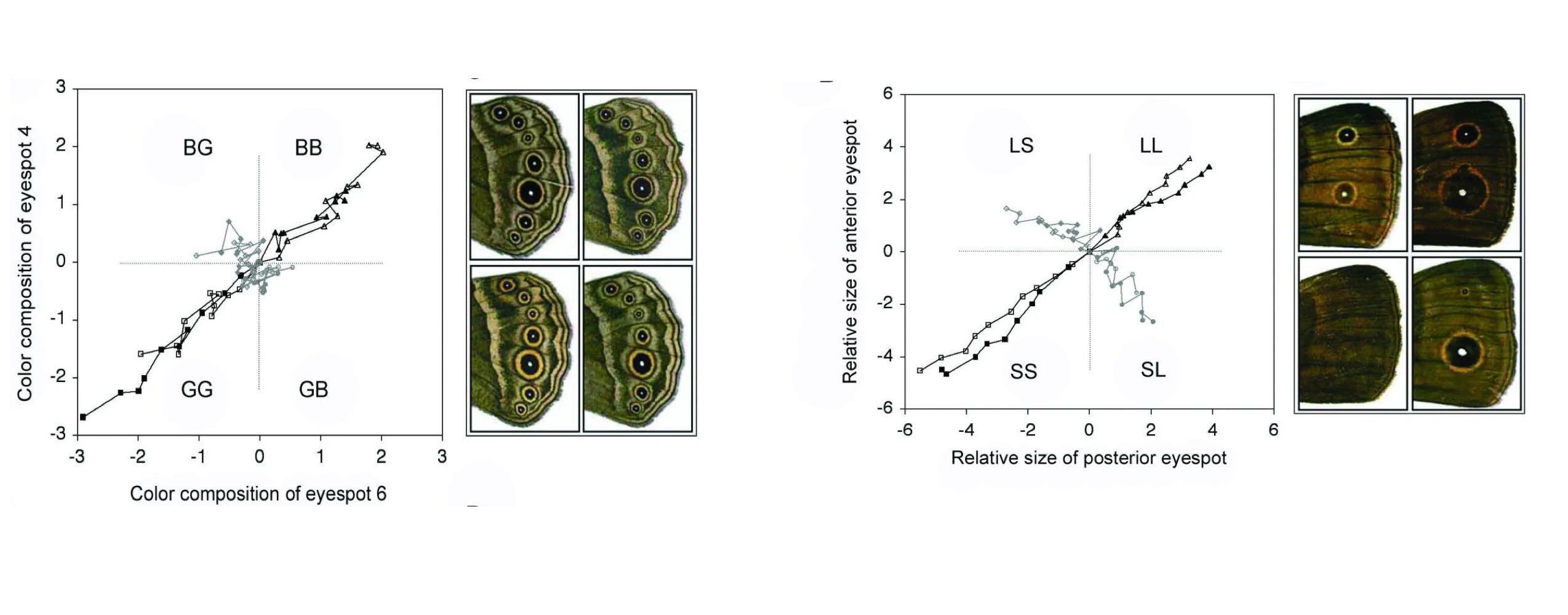Developmental constraints on learning (Allen et al. 2008). The eye spots on butterfly wings are correlated in both size and colour. Artificial selection cannot break the correlation between the colours (left), but it can break the correlation between the sizes (right).

The difference in flexibility suggests that the colour and size of eyespots are determined by different developmental mechanisms. This is indeed the case. During development, eyespot size is regulated by signalling from clusters of ‘‘organiser’’ cells. Each eyespot has its own organiser, and its mature size will therefore be relatively independent from that of neighbouring eyespots. Eyespot colour, on the other hand, develops in response to the concentration gradient of a diffusive signal. This concentration cannot be regulated independently for each eyespot, and neither can the response to any given concentration. Neighbouring eyespots are therefore bound to have similar colours.

The different causes of phenotypic correlations would have been difficult to predict from observational data alone, since the correlation across eyespot colour and size are similar in wild type butterflies (Allen et al. 2008). These experiments therefore not only show that either selective pressure or genetic constraints might play a role, they also show that disambiguating the two requires causal experiments.

Benefits of low-dimensionality

Low-dimensionality sounds like a limitation, but it can actually be an advantage as well, for instance when it provides robustness to noise and other sources of variability. Neuroscientists have long known the importance of so-called attractor dynamics: A Hopfield network converges to a previously imprinted attractor state, starting from an initial state that is similar to the attractor. The network therefore is robust to missing or noisy information. Similarly, attractor dynamics can make the formation of a decision robust to irrelevant information, as shown recently by Finkelstein et al..

Attractor dynamics are also thought to increase developmental robustness. For instance, cells adopt one out of many possible cell types, characterised by a reliable set of properties and functions. This type of ``canalisation’’ makes development robust to genetic and environmental variability (Waddington 1942, Flatt 2005). This idea is consistent with the aforementioned work on the one-dimensional Drosophila wings (Alba et al. 2021). In that work, genetic and environmental perturbations led to variation along the first principal direction, suggesting their effect is canalised by development.

Attractor dynamics can therefore steer neural activity or development towards one of a discrete number of states, and away from intermediate states. This decreases dimensionality, and that’s a good thing, since it allows neural computation or development to resist disturbing influences. Low-dimensionality can do even more, by improving the generalization of neural networks (Beiran et al. 2021).

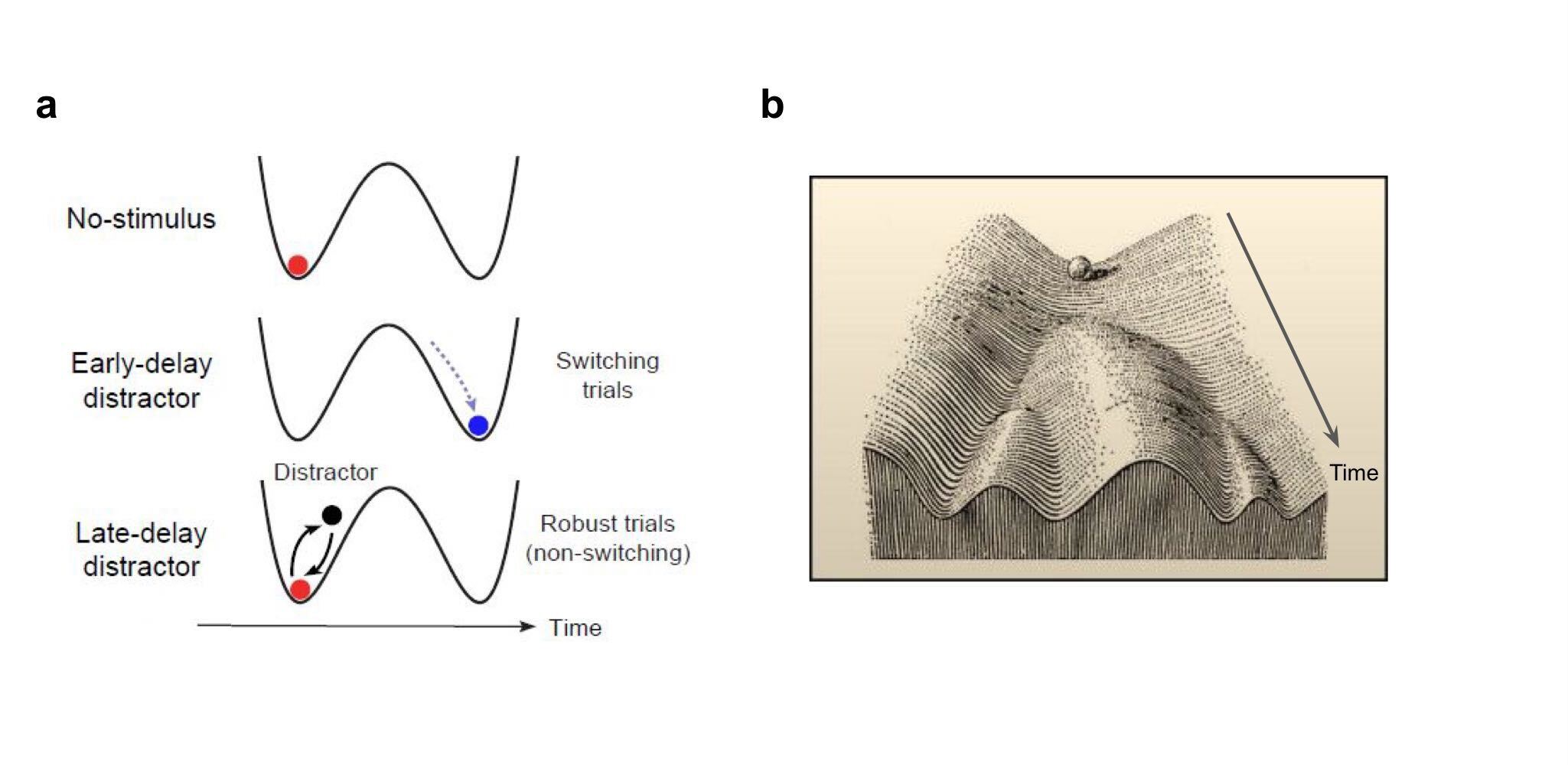(a) Attractor dynamics can increase the robustness of neural activity during decision making. The black curve represents the energy landscape, the ball represents neural activity following the curve’s gradient until it ends up in an attractor state. (b) Attractor dynamics can similarly increase the robustness of developmental processes to genetic and environmental variability. This is visualized here in Waddington’s epigenetic landscape. The ball represents a developing cell, which becomes progressively committed to a particular identity. (a) From Finkelstein et al. 2021, (b) from Waddington 1957

Counterpoint: the case for high-dimensionality

So far, we’ve emphasised low-dimensionality, but neural activity can also be high-dimensional. Using large (very large) scale neural recordings and sophisticated maths, Stringer et al. showed that the dimensionality of V1 activity is, in fact, as high as possible given smoothness requirements. Intuitively, extremely high-dimensional activity requires that neurons are sensitive to minute details of the stimulus. Even the slightest change would then completely change neural activity, making the neural code fragile. The need for robustness therefore limits the dimensionality of neural representations. But neural representations also shouldn’t be too low-dimensional, since this would make them insensitive to visual details. The key finding from Stringer et al., then, was that neural dimensionality seems to strike a near-optimal balance between robustness and efficiency. A follow-up paper showed that imposing a similar structure on artificial neural networks can actually make them more robust to adversarial examples (Nassar et al. 2021) – one of the more direct ways in which neuroscience has recently inspired artificial intelligence.

Finally, it can be a mistake to focus on a few high-variance dimensions. The fact that other dimension capture only a small percentage of the total variance doesn’t mean they don’t matter. The lab of Mark Churchland has shown that motor cortical dimensions predictive of muscle activity can actually explain relatively little variance (Russo et al. 2019), even though they clearly contribute to behaviour! It might therefore be better to assess a dimension’s relevance based on its trial-to-trial reliability, rather than the variance it explains (Stringer et al. 2019, Marshall et al. 2021).

Takeaways for neuroscience

The analogy between neuroscience and comparative biology suggests several lessons for neuroscience. First, computational neuroscientists tend to think of evolution (and development) as yet another optimisation process. But here we have seen that animals and their brains are not just shaped by adaption, they’re also shaped by constraints. We therefore cannot assume that each experimental observation has an adaptive explanation – adaptation is an assumption that requires testing4. Such a test might require causal experiments, as shown by the butterfly example.

Second, identifying a role for neural constraints is only a first step, the second step is identifying the mechanism causing the constraints. This was possible in the butterfly because it is a relatively simple and well-studied model organism. Determining mechanisms of neural constraints might similarly require a model organism that is more experimentally accessible than, for example, a primate.

A third takeaway is that low-dimensional structure should be taken into account when designing and interpreting perturbation experiments. The attractors in Waddington’s landscape, for example, are caused by gene regulatory networks. Perturbing one of the network’s member genes might not change overall gene expression all that much, leading us to conclude that the gene in question is not regulating cell identity. But actually it is, just not by itself. Interpretable causal experiments therefore require perturbations at the right level, as eloquently pointed out by Jazayeri & Afraz.

Finally, it would be interesting to see how evolutionary and neural manifolds interact, because the brain’s structure (phenotype space) influences its activity (neural space), and, conversely, the brain’s activity can influence its evolution by shaping behavior.

Acknowledgements

Thanks to Robert Lange for feedback on this post and encouragement to start blogging in the first place.

  1. In the neuroscience literature, ‘‘manifold’’ often refers to a subspace identified using something like principal component analysis. But manifold just sounds cool, doesn’t it. ↩

  2. Interpretability is perhaps the key reason why low-dimensionality matters, since thinking about high dimensions is hard. As Geoffrey Hinton said:``To deal with a 14-dimensional space, visualize a 3-D space and say ‘fourteen’ to yourself very loudly. Everyone does it.’’ ↩

  3. The actual procedure for training the subjects and calibrating the BCI was a bit more complicated (see Methods from Sadtler et al. 2014). If you think training a deep network is hard, try training a non-human primate! ↩

  4. The relative importance of adaptation versus other non-adaptive evolutionary processes is a actually a classical debate in the field. See the famous spandrels paper from Gould & Lewontin for a provocative contribution. ↩